Construct the Square Root of 2

The construction of the square root of 2 is based on the Pythagorean Theorem (see Euclid's Postulate 47). Take the premise of the Pythagorean Theorem: A2 + B2 = C2. How can we derive √2?

We can rewrite the equation as C = √(A2 + B2). If we let A = B, we get C = √(A2 + A2) = √(2A2). If we then let A = 1, we get C = √(2(1)2) = √(2). This means that if we construct an Isosceles Right Triangle with the sides A and B of length one (or unity), the length of the hypotenuse will be √2.

DiagramInstructions
Line AB is unity.

1. Let the line segment AB be unity (a line segment of length 1).

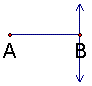Construct a line perpendicular to AB at B.

2. Construct a line perpendicular to AB at B.

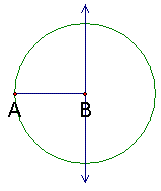Construct a circle with center B and radius AB.

3. Construct a circle with center B and radius AB

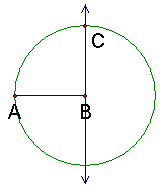Label an intersection of the perpendicular line and the circle as C.

4. Mark one intersection of the circle and the perpendicular line C.

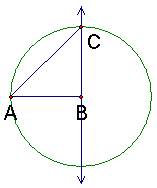Draw the segment AC. The length of segment AC is square root of 2.

5. Draw line segment CA. The length of line segment CA is √2.
Sorry, this page requires a Java-compatible web browser.

You can change the figure by clicking and dragging on points A and B. Notice that while the measure of the length of AB changes, the ratio of the length of CA to AB is always √2.

Proof

  1. The length of AB is taken to be 1 by definition.
  2. Since the segments AB and BC are both radii of the same circle, they are congruent, making BC of length 1.
  3. Since AB is perpendicular to BC (see Euclid's Proposition ??), ∠ CBA is a right angle.
  4. By the Pythagorean Theorem (see Euclid's Proposition 47), AB2 + BC2 = AC2.
  5. But, since AB and BC are unity, AB = BC = 1.
  6. 12 + 12 = AC2
  7. 1 + 1 = AC2.
  8. 2 = AC2.
  9. AC = √2, QED.

Citation

Cite this article as:
McAdams, David, Construct the Square Root of 2, from LifeIsAStoryProblem.org, 30 June 2007, , URL https://lifeisastoryproblem.tripod.com/numbers/cons_sqrt_2.html.

Printable Version

Download a printable version.