Construct the Square Root of 5

This construction uses the constructions of √2 and √3. The algebraic formula is (√2)2 + (√3)2 = (√5)2.

DiagramInstructions
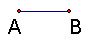Line segment with end points labeled 'A' and 'B'. 1. Let line segment AB be unity (a line segment of length 1).
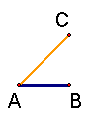Constructed line AC that has a length of square root of 2. The details are omitted since they are covered in cons_sqrt_2.html. 2. Construct √2 using AB as unity. How?
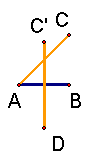Add constructed line C'D that uses AB as unity. 3. Construct √3 using AB as unity. How?
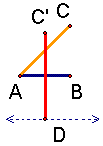Add a line parallel to AC through point D. 4. Draw a line parallel to AB through point D.
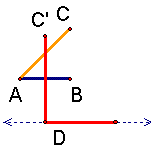Construct a line segment on the parallel line through D with endpoint D and a length of AC. 5. Draw a line of length AC with endpoint D in the parallel line.
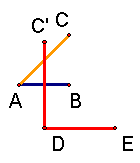Mark the endpoint of the line segment just drawn and label the end point 'E' 6. Mark the other endpoint of the line just drawn as E.
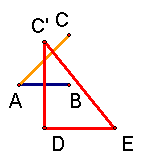Add a line segment C'E. 7. Draw line segment C'E. The length of C'E is √5.

You can change the figure by clicking and dragging on points A and B. Notice that while the measure of the length of AB changes, the ratio of the length of C'E to AB is always √5.

Proof

  1. The length of AB is taken to be 1 by definition.
  2. By construction, the length of AC is √2.
  3. By construction, the length of C'D is √3.
  4. Since DE is constructed to be the same length as AC, the length of DE is √2.
  5. By the Pythagorean Theorem (see Euclid's Proposition 47), DE2 + C'D2 = C'E2.
  6. By substitution, we get (√2)2 + (√3)2 = C'E2.
  7. By simplifying, we get 2 + 3 = C'E2.
  8. 5 = C'E2.
  9. √5 = C'E

Citation

Cite this article as:
McAdams, David, "Construct the Square Root of 5", from LifeIsAStoryProblem.org, 30 June 2007, , URL https://lifeisastoryproblem.tripod.com/numbers/cons_sqrt_5.html.

Printable Version

Download a printable version.